Hàm số liên tục là gì? Các định lý cơ bản của hàm số liên tục

Hàm số liên tục là một phần kiến thức quan trọng trong chương trình toán học. Để làm được bài tập bạn cần nắm vững lý thuyết cũng như các tính chất cơ bản. Vậy hàm số liên tục là gì? Hàm số liên tục có những định lý cơ bản nào? Các bạn hãy tham khảo bài viết dưới đây của Blog Số Đề để hiểu chi tiết hơn về hàm số liên tục.

Hàm số liên tục là gì?

Trong Toán Học, khi một hàm số được gọi là liên tục tức là nó không có sự thay đổi đột ngột về giá trị. Đây được gọi là những điểm gián đoạn của hàm số. Cụ thể khi đầu vào của hàm số thay đổi ít thì hàm số sẽ có sự chênh lệch đầu ra cũng nhỏ. Khi một hàm số không liên tục thì được gọi là gián đoạn.

Khi học lên chương trình cao hơn bạn sẽ được tìm hiểu về hàm số liên tục toán cao cấp, hàm số liên tục casio. Đến đây khái niệm về hàm số liên tục lại được hiểu theo một cách trừu tượng khác.

Hàm số liên tục tại một điểm

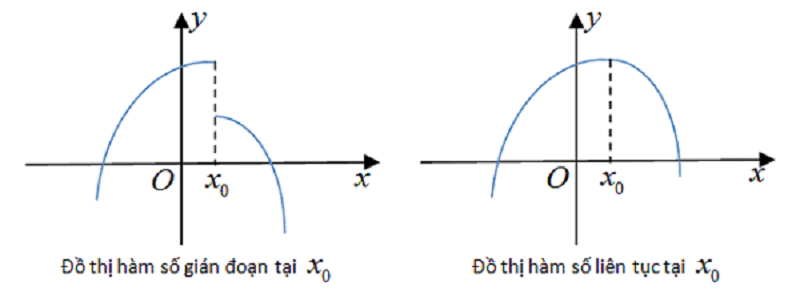
Cho một hàm số y = f(x) được xác định trên một khoảng (a;b) và x0 thuộc (a;b). Khi đó hàm số f(x) sẽ liên tục tại x0 khi: Lim[x→x0] f(x) = f(x0). Khi hàm số không liên tục tại điểm x0 thì thể gọi là hàm số đang gián đoạn tại x0.

Giả sử các hàm số y = f(x), y = g(x) được coi là liên tục tại điểm x0. Khi đó:

• Các hàm số y = f(x) + g(x) và y = f(x) – g(x), y = f(x).g(x) sẽ liên tục tại x0.

• Hàm số y = f(x)/g(x) sẽ liên tục tại x0 nếu g(x0) khác 0.

Hàm số liên tục tại một khoảng

Ta có hàm số y = f(x) sẽ liên tục trên khoảng (a;b) khi nó liên tục tại các điểm nằm thuộc khoảng đó. Khi hàm số đã cho liên tục trên khoảng (a;b) thì tương ứng trên khoảng đó, đồ thị của hàm số sẽ là một đường nét liền liên tục và không bị đứt.

Hàm số liên tục tại một đoạn

Hàm số y = f(x) được coi là liên tục trên đoạn [a;b] khi nó liên tục trên mọi điểm tại khoảng (a;b) và khi đó: limx→a + f(x) = f(a), limx→b − f(x) = f(b).

Các định lý cơ bản của hàm số liên tục là gì?

Để giúp bạn đọc hiểu sâu hơn về hàm số liên tục. Dưới đây Monkey đã tóm lược ngắn gọn những kiến thức về định lý của hàm số liên tục. Hãy cùng theo dõi để làm bài tập tốt hơn nhé!

Định lý 1

• Hàm số đa thức liên tục trên toàn bộ tập hợp số thực R.

• Hàm số lượng giác và hàm số phân thức hữu tỉ (thương của hai đa thức) liên tục trên từng khoảng của tập xác định của chúng.

Định lý 2

Giả sử: Hàm số y= f(x) và y= g(x) là 2 hàm số liên tục tại x. Ta có:

• Các hàm số y= f(x) + g(x), y= f(x) – g(x) và y= f(x). g(x) liên tục tại x;

• Hàm số y = f(x)g(x) liên tục tại điểm x nếu g(x) 0.

Định lý 3

Nếu hàm số y= f(x) liên tục trên đoạn [a;b] bất kì và f(a). f(b)

Định lý này được áp dụng để chứng minh sự tồn tại nghiệm của phương trình trên một khoảng và nó còn được phát triển dưới dạng khác như sau:

Hàm số y= f(x) liên tục trên đoạn [a;b] và f(a). f(b)

Các dạng toán về hàm số liên tục thường gặp

Để củng cố thêm kiến thức về hàm số liên tục, dưới đây Monkey xin giới thiệu đến bạn một số dạng toán thường gặp về hàm số liên tục

Dạng 1: Xét tính liên tục của hàm số tại một điểm cụ thể.

Để xét được tính liên tục của một hàm số đã cho trước tại điểm x0 ta thực hiện lần lượt các bước:

• Bước 1: Kiểm tra xem hàm số đã cho có xác định trên một khoảng chứa x0 hay không sau đó hãy tính giá trị tại f(x0).

• Bước 2: Tính limx→x0f(x). Trong nhiều trường hợp ta cần tính limx→x0 + f(x), limx→x0 – f(x).

• Bước 3: So sánh limx→x0f(x) với f(x0) và kết luận.

Dạng 2. Xét tính liên tục của hàm số trên một khoảng

Để xét tính liên tục hoặc xác định giá trị của tham số để hàm số liên tục trên khoảng I, chúng ta thực hiện theo các bước sau:

• Bước 1: Xét tính liên tục của hàm số trên các khoảng đơn.

• Bước 2: Xét tính liên tục của hàm số tại các điểm giao.

• Bước 3: Kết luận

Dạng 3: Ứng dụng hàm số liên tục chứng minh phương trình có nghiệm

Đầu tiên ta cần áp dụng định lý: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] cho trước và f(a).f(b) nhỏ hơn 0, thì phương trình f(x) = 0 sẽ luôn có ít nhất 1 nghiệm nằm trong khoảng (a; b).

Các bước cụ thể để làm bài chứng minh phương trình có nghiệm như sau:

• Bước 1: Biến đổi phương trình đã cho cần chứng minh về dạng f(x) = 0.

• Bước 2: Tiếp theo cần tìm 2 số a và b (a nhỏ hơn b) sao cho f(a).f(b) nhỏ hơn 0

• Bước 3: Cuối cùng chứng minh hàm số y = f(x) luôn liên tục trên đoạn [a; b] đã cho.

Kết luận

Bài viết trên Blog Số Đề đã chia sẻ đến các bạn về khái niệm hàm số liên tục là gì và những kiến thức có liên quan. Mong rằng điều này sẽ giúp ích rất nhiều cho bạn trong quá trình học tập. Hãy nhanh chóng rèn luyện thật kỹ những dạng toán trên để bản thân tích lũy cho mình nhiều kiến thức toán học hữu ích.

Tags liên quan: